¿Qué es más importante en matemáticas? ¿Aprender fórmulas y mecanizarse o entender unos pocos principios? La clave en matemáticas son sus principios básicos, no aprender fórmulas.
Ya ha pasado más de un mes desde que los escolares empezaron sus clases virtuales en el colegio. Vuelven los cursos fundamentales de la currícula, entre ellos las matemáticas.
Un día, uno de mis hijos se me acercó y me explicó unos de sus ejercicios de matemáticas. Lo hizo bastante bien. Seguidamente, le pregunté por qué procedió de la forma que lo hizo para resolver el ejercicio. No me supo contestar. En lo personal, me gustan mucho los números y fue por esa razón que traté de explicárselo de la manera más sencilla y lógica posible, de tal manera que sea fácil para él entender y hacer suya la idea. Claro está que no a todos los padres les gustan las matemáticas.
Principios básicos
Una de las ideas básicas o principios que existen en la naturaleza es el equilibrio. El principio del equilibrio o balance también es válido en las mátemáticas. La clave en matemáticas son sus principios básicos. Imaginemos una balanza.

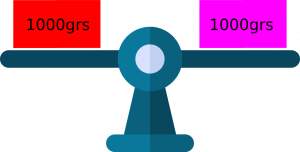
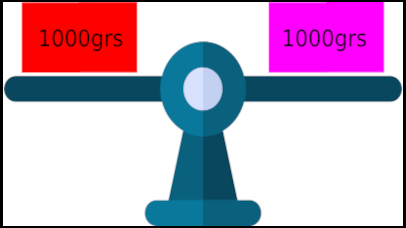
¿Qué pasaría si la balanza tiene 1000 grs de algo en uno de sus brazos y otros 1000 grs de algo en el otro?. La respuesta es obvia, ninguno de los brazos se inclina para ninguno de sus lados. Dicho de otro modo, la balanza se mantiene en equilibrio.
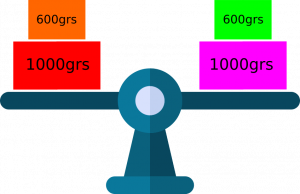
Ahora, ¿qué sucede si agregamos 600 grs de algo en uno de los brazos y otros 600 grs de otra cosa otro?. La respuesta también es evidente. Habrán 1600 grs en cada brazo de la balanza y por consiguiente se mantendrá el balance. «Si sumamos un peso igual a cada lado de la balanza, ésta se mantiene en equilibrio«. Denominemos como «Principio 1» esta propiedad para que después podamos referirnos a ella más adelante.
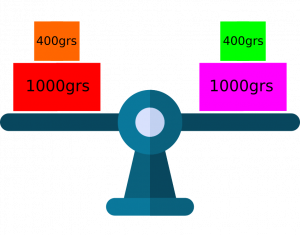
En este caso, ¿qué pasaría si quitamos 200 grs de cada brazo de la balanza?. La respuesta es la misma. Quedarán 1400 grs en cada brazo de la balanza. «Si quitamos o restamos un peso igual a cada lado de la balanza, ésta se mantiene en equilibrio«. Denominemos como «Principio 2» esta propiedad.
¿Qué pasa si duplicamos lo que contiene cada brazo de la balanza?. La respuesta sigue siendo la misma. «Si multiplicamos el contenido de cada lado de la balanza, ésta se mantiene en equilibrio«. Llamemos «Principio 3» esta propiedad.
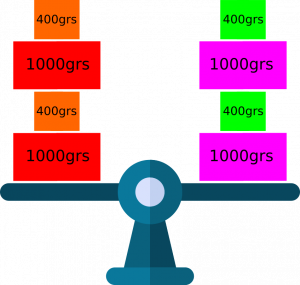
Finalmente, ¿qué es lo que pasa si nos quedamos con la mitad del peso de cada brazo de la balanza?. La respuesta sigue siendo la misma. La balanza está en equilibrio con 1400 grs en cada uno de sus brazos. «Si dividimos el peso de cada lado de la balanza, ésta se mantiene en equilibrio«. Llamemos esta propiedad «Principio 4«.
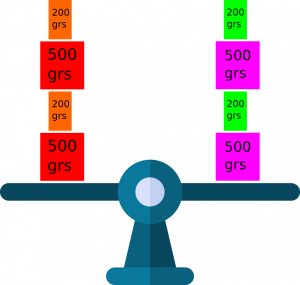
En esencia, se se trata de un mismo principio:
- Si sumas a un lado, sumas al otro.
- Si restas a un lado, restas al otro.
- Si multiplicas a un lado, multiplicas al otro.
- Si divides en un lado, divides también al otro.
Veamos a continuación algunos casos típicos.
Ejemplo de aplicación del Principio 1:
X – 50 = 30 .............. (1)
Mi hijo dijo que para determinar el valor de la X, simplemente el «-50 pasa al otro lado con +50». Le pregunté por qué pasa con signo cambiado. Él me respondió «porque sí».
Le enseñé entonces el Principio 1. En un lado de la balanza está X – 50 y en el otro el 30.
Sumemos 50 a cada lado, le dije
X - 50 + 50 = 30 + 50 .....(2)
El -50 + 50 se hacen cero porque al ser opuestos, al sumarse se anulan.
X = 30 + 50 ...............(3)
Compara el (1) con el (3).
¡Papá!, ahora ya sé por qué el -50 pasa al otro lado con el signo cambiado. ¡Muy bien hijo! le respondí. De ahora en adelante lo podrás hacer de frente con la diferencia de que ahora ya sabes por qué se hace así.
Un ejemplo con el Principio 2:
X + 90 = 120 ............. (1)
Ahora lo hago yo, dijo mi hijo. Aplico el caso en el que quito la misma cantidad a cada brazo, ¿verdad?. Yo asentí.
Restamos 90 a cada lado, me dijo, así la balanza se mantiene en equilibrio. ¡Excelente! dije.
X + 90 - 90 = 120 - 90 ....(2)
El 90 – 90 se hacen cero porque al ser opuestos, al restarse se anulan.
X = 120 - 90 ..............(3)
¡Mira papá!, es como si el 90 hubiese saltado al otro lado restando.
Hijo, veamos dos ejemplos más.
Ejemplo con el Principio 3:
20 X = 60 .............(1)
Papá, ya sé, el 20 pasa al otro lado restando. Le respondí, hijo, observa bien. ¿Qué dice el lado izquierdo de la balanza? Pues 20X y eso ¿qué significa? le pregunté. Me respondió 20 veces X. ¡Ah! papá, es una multiplicación, el 20 multiplica a la X. ¡Bien! exclame.
Divide entre 20 cada lado le dije. Papá, ¿por qué entre 20 y no otro número? me preguntó. Le respondí que según el ejercicio podría ser otro número, para este caso el 20 es el adecuado. ¿Por qué? me preguntó. Porque lo que quiero es saber el valor de una sola X. 20 entre 20 es igual a 1 me dijo. Me quedaría 1X que es lo mismo que decir X. ¡Ah! exclamó mi hijo.
20 X / 20 = 60 / 20 .....(2)
20 entre 20 es igual a 1 me dijo. ¡Ah!
X = 60 / 20 ............(3)
Papá, esta vez el 20 es como si hubiese pasado a dividir el otro lado. Asentí, pero ya sabes que eso es en términos prácticos. Lo importante es saber… ¡Si papá! ahora ya se la razón. Los números no saltan de un lado a otro, solo mantengo la balanza equilibrada. ¡Excelente! exclamé.
Hagamos un último ejemplo hijo, de acuerdo papá, contestó.
El útimo ejemplo con el Principio 4:
X / 40 = 6 .............(1)
Multipliquemos por 40 cada lado. Así de esa manera 40 / 40 da 1. ¡Magnífico! hijo
40 X / 40 = 6 x 40 .....(2)
X = 6 x 40 .............(3)
Papá, es como si el 40 hubiese pasado multiplicando. Ahora ya puedo resolver los ejercicios sólo, sabiendo lo que estoy haciendo. Eso es lo más importante ¡hijo! ¡Gracias papá ahora ya entiendo por qué la clave en matemáticas son sus principios básicos!
Intelecto espera que este artículo les sea de utilidad.
Podrás encontrar más ayuda sobre números en este enlace.



One Comment
Liz
¡Excelente explicación!